헤더파일
셰이더 공부 - 난반사광 본문
빛이 없으면 물체를 볼 수 없습니다.이 당연한 사실을 자주 까먹는 이유는 실생활에서 완전히 칠흑 같은 어둠을 찾기 힘들기 때문입니다. 왜일까요? 바로 끝없이 반사하는 빛의 성질 때문입니다. 딱히 눈에 띄는 광원이 없더라도 대기중의 미세입자에 반사되어 들어오는 빛까지 있으니까요.이렇게 물체에 반사되어 들어오는 빛을 간접광이라 하고 광원으로 부터 직접 받는 빛을 직접광이라 합니다.
이 두가지 빛 중 간접광은 수 많은 반사를 거쳐야 하기 때문에 계산하기 매우 어렵습니다. 따라서 이번에는 직접광만을 계산할 것입니다.
난반사광(Diffuse Light)
스스로 빛을 내지않는 물체를 우리가 볼 수 있는 이유는 다른 물체가 발산하는 빛이 이 물체의 표면에서 반사되기 때문입니다. 이때, 여러 방향으로 고르게 반사되는 빛이 있는데 이것을 난반사광이라고 합니다. 어느 방향에서 봐도 물체의 명암이나 색조가 크게 변하지 않는 이유가 이 난반사광 덕분입니다.
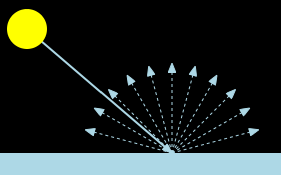
난반사를 계산하기 위해 게임에서 주로 사용하는 람베르트 모델을 사용합니다. 모델의 표면법선과 입사광이 이루는 각의 코사인 값이 난반사광의 양이라는 공식입니다.
법선이란 표면의 방위를 나타내는 벡터 값으로 평평한 평면에서 법선은 위쪽으로 수직인 선입니다. 보통 모델파일은 정점마다 법선벡터를 가지고 있습니다. 두 벡터가 이루는 각이 0일때 난반사광의 세기는 1로 가장 세지고 90도보다 작아진다면 0이하가 되어 난반사광이 없어집니다. 하지만 코사인함수는 그다지 값싼 함수가 아닙니다. 그래서 대안으로 내적연산으로 코사인을 대신하여 계산합니다. 약간의 수학공식이 들어갑니다.
● = 내적(Dot)
|A| = 벡터 A의 길이
|B| = 벡터 B의 길이
A●B = cosθ x |A| x |B|
즉 cosθ = A●B ÷ (|A| x |B|)
두 벡터를 단위 벡터 (길이가 1인 벡터) 라고 가정하면 cosθ = A●B 가 됩니다.
벡터의 값을 맘대로 바꿔도 되는 이유는 난반사광을 계산할 때 법선의 길이나 입사광벡터의 길이는 전혀 영향이 없기 때문입니다. A가 (a,b,c) B가 (d,e,f)라 했을 때 내적은 (a x d) + (b x e) + (c x f) 로 훨씬 쉽게 계산됩니다.
1.정점셰이더
struct VS_INPUT
{
float4 mPosition : POSITION0;
float3 mNormal : NORMAL;
};
struct VS_OUTPUT
{
float4 mPosition : POSITION0;
float3 mDiffuse : TEXCOORD1;
};
float4x4 gWorldMatrix;
float4x4 gViewMatrix;
float4x4 gProjectionMatrix;
float4 gWorldLightPosition;
VS_OUTPUT vs_main( VS_INPUT Input )
{
VS_OUTPUT Output;
Output.mPosition = mul( Input.mPosition, gWorldMatrix );
float3 lightDir = Output.mPosition.xyz - gWorldLightPosition.xyz;
lightDir = normalize(lightDir);
Output.mPosition = mul( Output.mPosition, gViewMatrix );
Output.mPosition = mul( Output.mPosition, gProjectionMatrix );
float3 worldNormal = mul(Input.mNormal, (float3x3)gWorldMatrix);
worldNormal = normalize(worldNormal);
Output.mDiffuse = dot(-lightDir, worldNormal);
return( Output );
}
struct VS_INPUT
{
float4 mPosition : POSITION0;
float3 mNormal : NORMAL;
};
float4 gWorldLightPosition;
일단 이번에는 텍스처를 사용 안 할 것이므로 uv좌표는 입력받지 않습니다. 대신 정점셰이더에서 법선벡터 좌표값을 받습니다. 추가로 내적연산을 위한 광원의 위치 값도 전역변수로 받습니다.
입사광의 벡터와 법선벡터와의 내적은 어느 셰이더에서 해도 상관 없습니다. 하지만 정점셰이더가 픽셀셰이더보다 훨씬 적게 불리기 때문에 정점셰이더에서 하는게 성능상 유리합니다.
float3 lightDir = Output.mPosition.xyz - gWorldLightPosition.xyz;
lightDir = normalize(lightDir);
입사광 벡터 값은 광원의 위치에서 현재위치를 뺀 값입니다. 여기서 한가지 더 생각할 부분은 3D수학에서 올바른 결과를 얻으려면 모든 변수의 공간이 일치해야 한다는 것입니다. 정점셰이더에서 Input. mPosition은 지역공간에 있고 Outpur.mPosition은 마지막에는 투영공간에 있습니다.
광원의 위치는 월드공간에서 정의 되어 있으므로 입사광 벡터값은 월드행렬을 곱한직후에 계산합니다. 계산한 벡터 값(lightDir)을 normalize함수로 정규화 시켜 길이를 1로 만듭니다.
float3 worldNormal = mul(Input.mNormal, (float3x3)gWorldMatrix);
worldNormal = normalize(worldNormal);
정점데이터 안의 법선도 지역공간에 있으므로 mNormal 변수를 월드행렬과 곱해서 월드공간으로 변환해 줍니다. 법선벡터는 float3 형이므로 월드행렬을 (float3x3)형태로 캐스팅 해줍니다.
역시 벡터 값을 정규화 해줍니다.
Output.mDiffuse = dot(-lightDir, worldNormal);
lightDir 대신 -lightDir을 사용한 이유는 두 벡터의 내적을 구할 때, 화살표의 밑동이 서로 만나야 하기 때문입니다. lightDir을 그대로 쓰면 입사광벡터의 머리가 법선의 밑동과 만나므로 잘못된 결과를 발생시킵니다. 내적한 결과는 실수 하나이지만 그냥 대입시키면 알아서 float3형으로 만들어 줍니다.
struct VS_OUTPUT
{
float4 mPosition : POSITION0;
float3 mDiffuse : TEXCOORD1;
};
출력값을 보면 시멘틱이 왜 TEXCOORD1인지 궁금할 수 있습니다. 난반사광이라고 알려주는 적당한 시멘틱이 없기 때문에 기본적으로 8개(TEXCOORD0 ~ TEXCOORD7)의 슬롯이 있어 모자랄 일 없는 TEXCOORD를 사용합니다.
2.픽셀셰이더
정점셰이더에서 난반사광까지 계산해줬으니 픽셀셰이더에서 할 일은 그 값을 출력할 일밖에 없습니다.
struct PS_INPUT
{
float3 mDiffuse : TEXCOORD1;
};
float4 ps_main(PS_INPUT Input) : COLOR0
{
float diffuse = saturate(Input.mDiffuse);
return float4(diffuse,1);
}
float diffuse = saturate(Input.mDiffuse);
saturate함수는 0이하의 값을 0으로 1이상의 값을 1로 만들어주는 함수입니다. cos값이 0이하 일 수 있지만 색상 좌표에서 제일 작은 값은 0이고 cos값이 0이하라면 난반사광이 없기 때문에 이 값은 0으로 만듭니다.
return float4(diffuse,1);
float3형인 diffuse와 4차원 벡터의 마지막 값인 w값을 1로 지정해서 float4형 색상값을 반환합니다.
'DirectX' 카테고리의 다른 글
| 셰이더 공부 - 툰셰이더 (0) | 2018.02.25 |
|---|---|
| 셰이더공부 - 정반사광 (0) | 2018.02.25 |
| 셰이더공부 - 텍스쳐 매핑 (0) | 2018.02.23 |
| 셰이더 공부 - Color Shader (0) | 2018.02.23 |
| DirectX11 - 정점버퍼, 셰이더 생성 (0) | 2018.01.24 |



